Seeing force fields

In last week’s post, I provided some background on force fields – what they are, what creates them, and how we can sense them.  This is actually at the heart of my research.  Specifically, I try to find out what types of materials are magnetic, and under what conditions.  Sounds boring, I know.  So my job today is to convince you otherwise.

What if I told you that I built an apparatus that “sees” force fields?  I refer to it as a microscope, simply because it takes images of very tiny objects.  It is not however, a microscope in the often-used sense of the word: I don’t look through a set of lenses to focus on the object of interest.  

To explain how my “force microscope” works, recall the refrigerator magnets from last week.  You could only tell that they were magnetic because you had two of them, and they exerted forces on one another.  If you instead had one unknown chunk of material, you would need a second object – already known to be magnetic – in order to test if the unknown is also magnetic.  This is exactly how my microscope works.  I measure the magnetic and electric forces between the sample I am studying (the unknown) and a small lever (which I know to be magnetic and/or charged).  

The lever is like a really small diving board.  Really small.  Imagine a diving board as long as a human hair is wide.  That’s just about right.

The lever hovers just above an “unknown” sample.  Just as a diving board bends due to the force of a diver’s weight, this lever will bend when it experiences a force.  For example, by placing a tiny magnet on the end of the lever, I can detect magnetic forces.  Since like poles repel and opposite poles attract, the lever can sense if the sample is magnetic by deflecting, or bending.

A magnet on the end of the lever causes the lever to bend in response to magnetic forces.  This allows me to determine if a sample is magnetic.

Alternatively, I can put a little bit of electric charge on the end of this lever.  This allows me to sense electric forces.

 

If I put charge on the end of the lever, charges on the sample will attract or repel the lever.

Because it’s so tiny, the lever will bend in response to very small forces.  How small?  Consider the mass of a feather – about 1 gram.  Imagine it resting on your hand.  Not much force certainly, but still perceptible: you can feel some small amount of pressure on your fingertips.  This tiny lever can detect forces one trillion times smaller than that.  I’m not using “one trillion” as a colloquialism here… I mean it quite literally.  It’s obviously tough to draw a comparison to everyday experience here.  If I were to place a single red blood cell on the end of this cantilever, it would cause a huge amount of bending, because even it is 100 times heavier than the smallest force the lever could detect.

Just to show you how cool this really is, here are a couple of images I’ve taken with my microscope.  

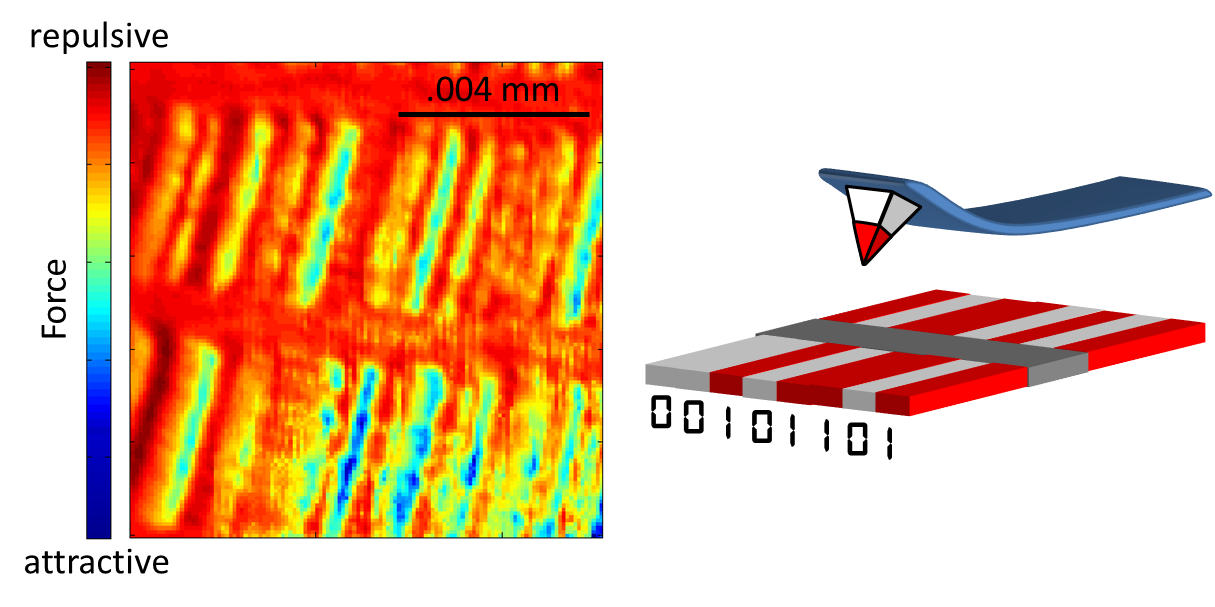The sample that I’m “looking” at here is a computer hard drive.  The cartoon at the right shows that a hard drive consists of magnetic regions: these are the 0s and 1s of digital information.  You see, inside your computer’s hard drive is a disc of literally billions of these tiny magnetic regions.  Their precise ordering (white-white-red-white-red-red-white-red OR 00101101, etc.) is how your songs, documents, and photos are saved.  For more about how binary code works, visit this video, and be sure to check out my favorite musical tribute to binary code.

On the left is the image of that hard drive obtained with my microscope.  The colors in the image aren’t the actual colors of the disc – remember: I’m not looking through a microscope with lenses.  Rather, this “false color image” is sort of like the weather radar map: the rain clouds aren’t actually red and green, but rather, the meteorologists use red to denote heavy rain and green for light rain.  I’m doing something similar here.  The color blue indicates an attractive force that pulls the lever towards the sample (just like two attracting refrigerator magnets).  Dark red is the opposite: a repulsive force pushing the lever away.  And just to provide a sense of scale, about 12 of these images could fit across the width of a human hair.  

Next, I show an image of a tiny electronic circuit.  The processors, or “brains”, of the computers, cell phones, and tablets that we use today have billions of circuits comprising them.  To fit that many circuits into a device that fits in the palm of your hand, those circuits must be very small.  The circuit we're looking at here is actually monstrous by those standards.  It measures about 10 micrometers across (one tenth the width of the human hair seen above).  In this space, you could fit 500 of the individual circuits used in a state-of-the-art Intel processor!

Remember in “Everything is a voltage” that charges are pushed around by voltages.  I like to think of voltages as hills and valleys that the charges roll through.  Well, that’s all that I’m doing with this simple circuit.  You can see in the bottom cartoon that I’ve hooked up a battery to the two arms of the micro-circuit.  The positive terminal of the battery “carries” positive charges to the top of the voltage “hill” and piles them up on the left arm of the micro-circuit (marked (+) because it has an excess of positive charge).  The charges then “fall down” to the lower voltage at the right arm of the circuit (connected to the negative terminal of the battery).  This is simply electrical current traveling from left-to-right.

A force image of a micro-circuit.  Gold wires connect to the circuit on the left and right sides.  Regions of high voltage create an attractive force, which is shown in black and purple.  Regions of low voltage exert little to no force on the lever (green and yellow).

The force image shows that the pile up of positive charges on the left arm causes a strong attractive force on the lever (which has a bit of negative charge on it).  This is the top of the voltage “hill”.  Moving from left to right you can see that the measured force becomes less attractive, and finally, at the right arm, we arrive at the bottom of the voltage hill where there is no force between the lever and the sample. You might have expected a repulsive force here (since the lever has a negative charge, and the right arm is connected to the (-) terminal of the battery).  However, I've also connected the (-) terminal of the battery to “ground” – that is, no charge.  Without any charge there, the lever doesn’t get repelled. So the colors of the image don't just indicate the force on the lever; you can also interpret them as the voltage at each spot in the device: black and purple represent high voltage, yellow and green are low.

This is one of my favorite pieces of data that I’ve collected during my research.  You and I can’t “see” voltages ordinarily.  We rely on “High Voltage” signs to warn us to keep back, and tiny (+) and (-) symbols informing us which way to install a battery.  We can't see the electrical pulses traveling up the mouse cable with every click, or the currents running through the wires connecting your earbuds to your phone.  But here we have an image that dramatically highlights the “hills” and “valleys” that cause electrons to travel through a circuit.

So the force fields that I use and measure in the lab aren’t exactly the impenetrable shields encountered by the rebels on their assault of the Death Star.  Maybe it takes the wind out of the sails a bit, but I still find them pretty cool.  For me, these images give textbook physics – voltages, magnetism, force fields – a sense of realness that cannot be captured otherwise.  They also keep me humble – no matter how busy I feel my life may be, there are so, so many atoms and electrons buzzing about keeping me alive, holding the “stuff” of everything together, dutifully obeying the laws of physics without complaint.  Some people enjoy turning their eyes skyward at night, perhaps peering through a telescope, to put into perspective the happenings of our lives on the grand stage of the universe.  I have found an entire other universe down at the microscopic level; one that often goes unnoticed, and is taken for granted.  And it is just as marvelous.

Force fields are real

Force fields made frequent appearances in the games that I played and the sci fi movies I watched as a kid (OK, continue to watch).  These fields usually protect a ship or soldier from the various forms of harm raining down upon them.  For example, in the video game “Scorched Earth” – an old favorite of mine – players competed as tanks, lobbing various munitions at one another.  Here you can see 6 tanks with force field shields around them.

A screenshot from the DOS classic Scorched Earth.

At some point growing up, force fields went the way of warp speed and the lightsaber – as far as I could tell, they existed only in the realm of science fiction.  So I distinctly remember sitting in my undergraduate E&M (Electricity and Magnetism) class and realizing “whoa, force fields are real.”  Now, as a research scientist, one of my primary focuses is to measure and even “see” force fields.  

So what do I mean that force fields are real?  What is a field even?  It’s admittedly tricky to describe what a field is.  It’s not really made of any thing.  It’s easier to instead describe what a field does.  In that sense, a field is simply the mechanism by which two or more distant objects interact.  They don’t touch.  But they can exert forces on each other through invisible fields.  It's easier to understand through examples.

You’re probably pretty comfortable with the idea of force fields, maybe without even knowing it.  Gravity pulls an apple to the ground.  This is because the apple experiences Earth’s unseen gravitational force field.  That same force field keeps the moon in orbit around the Earth.  

What other force fields exist?  Well, nearly everyone knows the expression “opposites attract.”  Although often referring to romance and dating, here I have in mind the electric fields created by charged objects.   A positive charge is attracted to a negative charge.  Conversely, two negative charges repel one another.  Like the Earth and the apple, there is no “stuff” connecting the charges.  Instead, a charge produces a field that extends out into space away from it.  This communicates to everyone nearby: “hey, I’m negative.  If you’re positive, come hang out.  If you’re negative, stay away!”

LEFT: A negative charge creates an electric field that points toward it.  This field gets weaker as you move farther from the negative charge. CENTER: The electric field produced by the negative charge exerts an attractive force on positive charges.  RIGHT: Other negative charges are repelled.

We rarely see the impact of electric force fields because most day-to-day objects are uncharged.  You and I are uncharged.  Sure, we’re made up of negative electrons and positive protons – but because there are an equal number of them, we have no net charge.  Your desk has no charge.  The air you breathe… you got it, neutral.  None of these objects can be pushed or pulled by electric fields.  However, there is a simple experiment that you can do to experience electric force fields: rub a balloon on your head.  Doing so transfers charge from your head to the balloon.  The balloon has now gained some charge – let’s say negative charges.  It grabbed these charges from your hair.  Because your hair has lost those negative charges, it is now positively charged.  Negative balloon.  Positive hair.  What happens? 

Now repeat with two balloons, rubbing both on your hair.  Both balloons will become negatively charged.  If you then gently rest one balloon in each hand and slowly bring your hands together… the balloons begin to interact, repelling one another.  They are experiencing one another’s force fields!

Similar behavior is found with magnets.  We’ve all played with refrigerator magnets: holding one in each hand and bringing them together slowly, we find one of two outcomes.  When they get close enough, they might snap together.  Or you might find that they want to wiggle away from one another.  Either way, they are interacting from afar.  We can’t see the force fields they are producing, but we can “feel” their effects as we bring the magnets together. 

Just like the charges, we can use the phrase “opposites attract” as the rule describing the behavior of magnets.  Unlike charges, which can be positive or negative, a magnet always has a pair of “charges” at its ends. We typically call these the magnetic poles: the north pole and the south pole.  The north pole of one magnet attracts the south pole of another.

In addition to being able to hold photos to your fridge, magnets are useful for navigation – at least they used to be.  Before GPS, the low-tech solution for wandering the woods or sailing the high seas was the compass needle.  Itself a magnet, a compass needle has both a north and a south pole.  And because Earth has a magnetic field (it too is just a giant magnet!), the magnetic compass needle feels a force that causes it to “point north."  A bit of trivia: since the north pole of your compass needle points to the Earth’s geographic Northern-most point, that point is actually a magnetic south pole.

Earth has its own magnetic field, which exerts a force on compass needles.  The north (red) pole of the compass needle is attracted by Earth's south magnetic pole, which actually is located at the geographic north pole.  Confusing, I know.

This cartoon starts to give you a sense of what to envision when you think of Earth’s magnetic field.  It extends from the Earth’s core out into space (not just outer space, but everywhere in space – where you’re sitting, and where the satellites orbit).  Just like the electric field of the negative charge shouted "hey, I'm negative," the Earth's magnetic field communicates "I'm magnetic" and exerts forces on other magnetic objects.  The large swooping arcs that connect the magnetic north pole to the south pole show what the magnetic field “looks like.”  We can’t see it of course.  But with another magnet – like a compass – we can detect it.  Earth has a force field!  It’s very real, and very measurable!

A simpler and more dramatic way to “see” the force field from a magnet is to sprinkle iron filings onto a tabletop, and then set the magnet down atop the filings.  The iron filings act like many small compass needles (iron is magnetic), each aligning itself to the line of magnetic force at that point in space.

Any old magnet produces a magnetic field similar to Earth's.  You can see this using either a compass needle, or by sprinkling iron filings around the magnet.

Permanent magnets aren’t the only way to produce magnetic fields.  Remember the coil of wire I was working on in “Seriously though, everything is a voltage”?  That coil is used to produce magnetic field.  Here’s how: when a current runs through a wire, a magnetic field appears, circulating around the wire.

You could test this by holding a compass nearby.  Depending where the compass is placed around the wire, the needle will point in a different direction.  Now imagine wrapping that wire around on itself to form a circular loop.  The magnetic field will continue to circulate around the wire.  But in the middle of the loop, all of those circulating fields point in the same direction – straight out of the loop.

A loop or coil of wire with an electric current running through it produces a magnetic field that points straight out of the loop.  This is how an MRI scanner produces a magnetic field.

An MRI scanner generates a magnetic field in just this way.  Your body is inserted into a huge coil of wire.  The current is flipped on, and now you find yourself sitting in a very strong magnetic field.  That’s the “M” in MRI – Magnetic Resonance Imaging.

So there you are sitting in a strong magnetic field, why don’t you feel any forces pushing or pulling on your body, trying to reorient you like a compass needle?  Well, just as humans aren’t electrically charged, we also aren’t very magnetic.  (We are a little bit magnetic, otherwise MRI wouldn’t work… let’s get into that another time). 

This all goes to show why we haven’t seen the force fields of science fiction.  While we certainly know how to produce force fields (charges, magnets, and current-carrying wires), the objects on which these fields exert forces are limited.  Magnetic fields exert forces only on magnetic objects (in other words, don’t carry a heavy wrench in your pocket during your MRI scan).  Electric fields can exert forces on electrically charged objects.  But since humans are neither magnetic nor charged, you can’t use E&M fields to put up a shield that keeps other people out.  The same is true for incoming enemy fire – a magnetic or electric force field won’t protect you.

But that doesn’t mean force fields aren’t very real, and very useful.  We use magnetic fields all of the time.  Any time you listen to music, watch TV, or listen to a call on your cell phone, magnetic fields push and pull on speaker cones to generate sound.  Electric motors use magnetic force fields to cause rotation: whether to spin the blades of your smoothie blender, roll up a car window, or swing the windshield wiper blades.  Earth’s magnetic field exerts forces on incoming electrons and protons – an effect which leads to the northern lights.  And remember how “Everything is a voltage”?  We learned that electrons can be pushed from high voltage to ground (like a ball rolling downhill).  That difference between high voltage and ground – that’s just an electric force field, pushing on the electrons.  Every time we use electricity, we are using electric force fields.  So much for science fiction.  Force fields are very much real. 

What's a watt?

You’ve likely heard of a watt – maybe you’ve replaced a 60 watt light bulb, or received your electricity bill and discovered that because you ran the AC too much last month, your household consumed 1200 killowatt-hours (900 kilowatt-hours is the average energy consumption of US households, per month).  Or maybe you’re into distance training and you hear people talk about “putting down some good watts.”  It’s difficult for me to conceptualize how much a watt is.  But I do know that a watt is related to energy consumption.  I also know eating is related to energy consumption.  And I know we measure food energy in calories.  Which takes me back to high school…

It was in my high school chemistry classroom that I first found myself excited by science.  And I’ll confess, one of the reasons… we got to burn stuff.  Seriously, we would set walnuts on fire.  Not just for fun, but for science!  We hear the lingo all the time… fat burning, carb burning, calorie burning.  It turns out, these metaphors are pretty much on the money.  When our bodies convert food to energy, the chemistry that happens is identical to burning, albeit more controlled.  Specifically, we break the carbon and hydrogen bonds in large molecules (like glucose), create new bonds with oxygen, and in the process get lots of energy out (as well as carbon dioxide, which we exhale, and water, which we, well, you know…).  

The "burning" of glucose creates energy (and carbon dioxide and water). 

In the case of metabolism, that energy allows our cells to go about their business keeping us alive.  In the case of fire, that energy is converted to light and heat: the flame.
 

So back to the burning walnuts.  In my chemistry class, we did a little experiment to measure the number of calories in a walnut.  We would do this by burning the walnut – quite literally – and capturing its heat output.  Check out the diagram below:

A simple experiment for measuring the caloric content of a nut.

This brings me to the actual definition of a food calorie: the amount of energy needed to raise the temperature of 1000 grams of water by one degree Celsius.  So to measure the number of calories in the walnut we would simply measure the temperature of a known amount of water before and after burning the walnut. 

 

In order to complete a half-ironman, I’m going to need a lot of energy, which means I’ll need to eat a lot of food (even during the race).  We are used to seeing energy content in food measured in calories.  

But there is an alternative way to measure energy stored in food – using joules.  Just as distance can be measured in either miles or kilometers, energy can be measured in calories or joules.  And as with distance measurements, where America seems to be the only place using miles, it would make things easier if we switched from calories to joules (you’ll see why in a bit).  There are 4,184 joules for each food calorie.  So that same Nutrition Label based on the units that nearly everyone else in the world uses would look like this:

Let me run with the distance analogy for a moment: Speed is a rate, measured in distance traveled per unit time (think: miles per hour, or meters per second).  Similarly, power – which is measured in watts – is a rate.  In this case, measured in joules per second.

This is why the joule is easier than the calorie to work with: it is very simply related to the watt.  

We’re finally set up to compare that 60 W light bulb to something a bit more tangible: the amount of energy we burn as humans, just by living.  Let’s do a quick calculation.  Let’s say you follow the USDA guidelines and consume 2000 calories per day.  To convert this to watts we have to run through some quick conversions – calories to joules (see, don’t you wish the USDA made its recommendations in joules?), and days to seconds.  That way we get an answer in joules per second, or watts.

 So you require just a bit more power than two standard 60 W light bulbs.

The human body consumes nearly 100 W of power when going about daily activities, like thinking at the office.  This is the equivalent power drawn by about 1.5 incandescent bulbs (60 W), or 7.5 compact fluorescent bulbs (13 W).

Now, to move that human body through the water, or to run or bike, you can guess that we NEED MORE POWER!

I can do a back-of-the-envelope estimate of how much power I must produce on the bike in order to hold a steady pace on a windless, flat road.  Remember Galileo and the two cyclists?  We learned that air resistance can be a big factor in cycling.  In fact, even on this windless road it is the primary force that I am working against.  To hold a constant speed, I must exert as much force to drive myself forward as the air resistance is pushing back against me with.  If I am going 20 mph… let me do some physics and math on the side here… I must produce 166 W of power.  I could power nearly 3 lightbulbs!  For comparison, elite cyclists can average 300 W of power, and can crank out more than 1,500 W in short bursts!

Hop on a bike and try to go 20 mph and you’ll need to produce an extra 166 W, on top of the 97 W your body already needs to perform its normal functions.

Now, let’s say I wanted to hold that pace for a 56 mi race (the bike leg of a half-ironman).  That can be easily divided by my 20 mph pace… it should take about 3 hours.  I just found that I have to produce 166 W of power to hold that speed.  So, my body will be using 166 joules every second for 3 hours.  

Sounds like a big number.  Let’s convert this to calories (since we are more familiar with that).  Remember that there are 4,184 joules per calorie, so we just divide our answer in joules by 4,184… I get 430 calories.  But here’s the kicker.  The human body isn’t a perfect food-to-mechanical energy conversion machine.  In fact, we are only about 20-25% efficient at converting food energy to motion.  So that means I will need 4 to 5 times that many calories in order to maintain that pace.  This is as much as 2150 calories!  Hence, this is what a typical grocery-store checkout looks like for me these days:

This brings me to my last point.  Since power is energy divided by time, we just saw that to calculate total energy consumed, we need to multiply power by time.  Or rearranging the equation we started off the day with:

 

This is why your electricity bill reports energy usage in kilowatt-hours.  It’s a weird unit.  I think we are used to saying things like “miles per hour” or “heart beats per minute.”  But in this case, we multiply your power use (in kilowatts) by the time of usage (in hours).  You can think of the hyphen in kilowatt-hours as a multiplication sign: kilowatt*hours.  Contrast this to miles per hour, where we think of “per” as the division sign.  Remember that watts are already in units of energy per time; so don’t read your energy bill as kilowatts per hour.  That would be the equivalent of saying “I drove my car at 60 miles per hour per hour.”  By instead multiplying wattage by time, we are left finally with energy.  So long story short, kilowatt-hours are a measure of energy, like joules, and no longer a rate, like watts. In fact, 1 kilowatt-hour is 3.6 million joules.

A 100 watt light bulb running for 10 hours consumes 1 kilowatt-hour of energy (100 watts * 10 hours = 1,000 watt-hours, or 1 kilowatt-hour).  Alternatively a 5000 W central air conditioner running for just 12 minutes also consumes a total energy of 1 killowatt-hour.  Below are some common appliances and gadgets, just to give you a sense of our energy-hungry lifestyles.  Remember that these are in watts: the rate at which these devices consume energy when they are on.  To find how much total energy they gobble up, you just multiply by their wattage by total running time.

Laptop	50 W
Microwave	1500 W
Clothes dryer	3400 W
Cell phone	1 W
Light bulb (incandescent)	60 W
Light bulb (compact fluorescent)	13 W
Central Air Conditioner	5000 W
Amateur Cyclist (like me)	100 – 200 W

So let’s take a look at that 1200 kilowatt-hour utility bill.  We can just multiply the power (1,200,000 watts) by one hour.  There are 3,600 seconds in an hour (60 minutes/hour * 60 seconds/minute).  This comes to be about 4 billion joules… that’s 4,000,000,000.  Or in calories: 1,032,505 – nearly one-and-a-half year’s worth of eating (on a 2,000 calorie diet)!